matte nøtter | Realfagshjørnet

MATTENØTT NR. 187 27. juli 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer denne månedens oppgave:

OPPGAVE 187 – MIDTPUNKTET I EN TREKANT

Gitt en vilkårlig trekant ABC. En median er en linje fra et hjørne til midt på motstående side. Alle deles i forholdet 2:1, der den lengste delen er nærmest hjørnet. Figur:

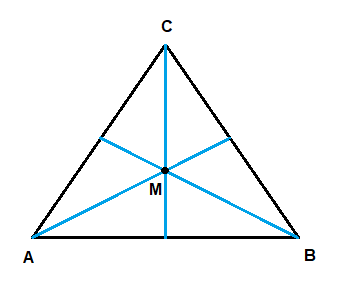
Medianene er de blå linjene. Vis at medianene møtes i midtpunktet M (tyngdepunktet) i trekanten. Figuren er kun en skisse. Man finner ingen opplysninger ved å forsøke å måle på figuren.

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 186 – TALLFØLGE II

Gitt en følge av tall der det første tallet er 2. Følgen er gitt ved

Vis at

Hint: Se OPPGAVE 159 – TALLFØLGE

JULENØTTER 2020

$x_{n+1} = x_n + 1$

$x_{n+1} - x_n = 1$

$r^n (r - r^0) = 0$

$r^n (r - 1) = 0$

$r - 1 = 0$

$r = 1$

$x_n^h = D \cdot 1^n = D$

$x_n^p = An^2 + Bn + C$

$x_{n+1} - x_n = 1$

$A(n+1)^2 + B(n+1) + C - (An^2 + Bn + C) = 1$

$A(n^2 + 2n +1) + B(n+1) + C - (An^2 + Bn + C) = 1$

$2An + A + B = 1$

$2A = 0 \indent \wedge \indent A + B = 1$

$A = 0 \indent \wedge \indent B = 1 - A = 1 - 0 = 1$

$x_n^p = An^2 + Bn + C = 0 n^2 + 1 n + C = n + C$

$x_n = x_n^h + x_n^p = D + n + C = n + E$

$x_1 = 1 + E = 2$

$E = 2 - 1 = 1$

$\Downarrow$

$x_n = n + E = n + 1$

Neste artikkel kommer i august. Hilsen erty56.

MATTENØTT NR. 186 26. juni 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer denne månedens oppgave:

OPPGAVE 186 – TALLFØLGE II

Gitt en følge av tall der det første tallet er 2. Følgen er gitt ved

$x_{n + 1} = x_n + 1 \indent der \ x_1 = 2 \indent (n \ge 1)$

Vis at

$x_n = 1 + n$

Hint: Se OPPGAVE 159 – TALLFØLGE

JULENØTTER 2020

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 185 – ULIKHETER

$\frac{11}{7} < x < \frac{15}{7}$

der x er et helt tall. Finn x.

$\frac{11}{7} = 1,5714286...$

$\frac{15}{7} = 2,1428571...$

Det eneste hele tallet mellom disse to er x = 2. Svaret er altså x = 2.

B) Gitt

$\frac{58}{35} < \frac{x + 24}{35} < \frac{12}{7}$

der x er et helt tall. Finn x.

$\frac{12}{7} = \frac{60}{35}$

$\frac{58}{35} < \frac{x + 24}{35} < \frac{60}{35}$

Det eneste hele tallet mellom 58 og 60 er 59.

$x + 24 = 59$

$x = 35$

Neste artikkel kommer i juli. Hilsen erty56.

MATTENØTT NR. 185 21. mai 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer denne månedens oppgave:

OPPGAVE 185 – ULIKHETER

A) Gitt

$\frac{11}{7} < x < \frac{15}{7}$

der x er et helt tall. Finn x.

B) Gitt

$\frac{58}{35} < \frac{x + 24}{35} < \frac{12}{7}$

der x er et helt tall. Finn x

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 184 – FUNKSJONER

A) Gitt funksjonene f(x) = 1/x og g(x) = x. Finn skjæringspunkter mellom f(x) og g(x).

Man finner skjæringspunkter mellom to funksjoner f(x) og g(x) ved å sette f(x) = g(x), og regne denne ligningen.

$f(x) = g(x)$

$\frac{1}{x} = x$

$\frac{1}{x} - x = 0$

$\frac{1 - x^2}{x} = 0$

$1 - x^2 = 0$

$x^2 = 1$

$x = \pm 1$

$x = -1 \indent \vee \indent x = 1$

$x = - 1$

$f(- 1) = \frac{1}{-1} = -1$

$x = 1$

$f(1) = \frac{1}{1} = 1$

Konklusjon: Skjæringspunktene er (x , y) = (-1 , -1) og (x , y) = (1 , 1).

Alternativt kunne man ha regnet ut g(-1) og g(1) for å finne skjæringspunktene. Man kan også finne skjæringspunktene ved å tegne grafene. Her er f(x) tegnet i blått og g(x) i rødt:

B) Gitt funksjonene h(x) = x³ + 2x² – 2x + 30 og t(x) = 8x² + 2x + 6. Finn skjæringspunkter mellom h(x) og t(x).

$h(x) = t(x)$

$x^3 + 2x^2 - 2x + 30 = 8x^2 + 2x + 6$

$x^3 - 6x^2 - 4x + 24 = 0$

Ser at x = 2 er en løsning, fordi

$2^3 - 6 \cdot 2^2 - 4 \cdot 2 + 24 = 8 - 24 - 8 + 24 = 0$

Utfører polynomdivisjon:

$\underline{(x^3 - 6x^2 - 4x + 24)} : (x - 2) = x^2 - 4x - 12$

$-(x^3 - 2x^2)$

$\underline{=(- 4x^2 - 4x + 24)}$

$-(-4x^2 + 8x)$

$\underline{=(- 12x + 24)}$

$-(-12x + 24)$

$= 0$

$\Downarrow$

$x^2 - 4x - 12 = 0$

$(x - 2)^2 = 12 + (-2)^2$

$(x - 2)^2 = 12 + 4$

$(x - 2)^2 = 16$

$\sqrt{(x - 2)^2} = \sqrt{16}$

$x - 2 = \pm 4$

$x = \pm 4 + 2$

$x = -2 \indent \vee \indent x = 6$

$x = - 2$

$h(-2) = (-2)^3 + 2(-2)^2 - 2(-2) + 30 = -8 + 8 + 4 + 30 = 34$

$x = 2$

$h(2) = 2^3 + 2 \cdot 2^2 - 2 \cdot 2 + 30 = 8 + 8 - 4 + 30 = 42$

$x = 6$

$h(6) = 6^3 + 2 \cdot 6^2 - 2 \cdot 6 + 30 = 216 + 72 - 12 + 30 = 306$

Skjæringspunktene mellom h(x) og t(x) er altså (x , y) = (-2 , 34) og (x , y) = (2 , 42) og (x , y) = (6 , 306) .

Alternativt kunne man ha regnet ut t(-2), t(2) og t(6) for å finne skjæringspunktene. Man kan også finne skjæringspunktene ved å tegne grafene.

Neste artikkel kommer i juni. Hilsen erty56.

MATTENØTT NR. 184 20. april 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer denne månedens oppgave:

OPPGAVE 184 – FUNKSJONER

A) Gitt funksjonene f(x) = 1/x og g(x) = x. Finn skjæringspunkter mellom f(x) og g(x).

B) Gitt funksjonene h(x) = x³ + 2x² – 2x + 30 og t(x) = 8x² + 2x + 6. Finn skjæringspunkter mellom h(x) og t(x).

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 183 – NOE VANSKELIG GEOMETRI

Gitt en syklisk firkant med sidene a, b, c og d. Vis at arealet er

$A = \sqrt{(s - a)(s - b)(s - c)(s - d)}$

der s er halve omkretsen.

Hint: Det finnes flere mulige løsningsforslag. Man kan f.eks. anvende vektorregning eller klassisk geometri.

Løsningsforslag:

Arealet av en trekant med sidene a og b er 1/2 multiplisert med sidene a og b og sinus til vinkelen mellom a og b. Figur:

$\displaystyle A = \frac{1}{2} \cdot a \cdot b \cdot sin \ \alpha + \frac{1}{2} \cdot c \cdot d \cdot sin \ \beta$

$\displaystyle A^2 = \frac{1}{4} \cdot a^2 \cdot b^2 \cdot (sin \ \alpha)^2 + \frac{1}{2} \cdot a \cdot b \cdot c \cdot d \cdot sin \ \alpha \cdot sin \ \beta$

$\displaystyle + \frac{1}{4} \cdot c^2 \cdot d^2 \cdot (sin \ \beta)^2$

$\displaystyle sin \ \alpha = sin \ \beta$

$\displaystyle A^2 = \frac{1}{4} \cdot (ab + cd)^2 \cdot (sin \ \alpha)^2$

$\displaystyle 4 A^2 = (ab + cd)^2 \cdot (1 - (cos \ \alpha)^2)$

$\displaystyle cos (\alpha + \beta) = cos \ 180^{\circ}$

$\displaystyle cos \ \alpha \ cos \ \beta - sin \ \alpha \ sin \ \beta = -1$

$\displaystyle cos \ \alpha \ cos \ \beta = (sin \ \alpha)^2 -1 = - (cos \ \alpha)^2$

$\displaystyle cos \ \beta = -cos \ \alpha$

Kaller den blå linjen e. Cosinussetningen gir

$\displaystyle e^2 = a^2 + b^2 - 2 \ a \ b \ cos \ \alpha = c^2 + d^2 - 2 \ c \ d \ cos \ \beta$

$\displaystyle - 2 \ a \ b \ cos \ \alpha + 2 \ c \ d \ cos \ \beta = c^2 + d^2 - a^2 - b^2$

$\displaystyle 2 \ a \ b \ cos \ \alpha - 2 \ c \ d \ cos \ \beta = a^2 + b^2 -c^2 - d^2$

$\displaystyle 2 \ a \ b \ cos \ \alpha + 2 \ c \ d \ cos \ \alpha = a^2 + b^2 -c^2 - d^2$

$\displaystyle 2 \ cos \ \alpha (ab + cd) = a^2 + b^2 -c^2 - d^2$

$\displaystyle cos \ \alpha =\frac{a^2 + b^2 -c^2 - d^2}{2(ab + cd)}$

$\displaystyle 1 - (cos \ \alpha)^2 = 1 - (\frac{a^2 + b^2 -c^2 - d^2}{2(ab + cd)})^2$

$\displaystyle 1 - (cos \ \alpha)^2 = \frac{2^2(ab + cd)^2 - (a^2 + b^2 -c^2 - d^2)^2}{2^2(ab + cd)^2}$

$\displaystyle 4 A^2 = (ab + cd)^2 \cdot (1 - (cos \ \alpha)^2)$

$\displaystyle 4 A^2 = (ab + cd)^2 \cdot \frac{2^2(ab + cd)^2 - (a^2 + b^2 -c^2 - d^2)^2}{2^2(ab + cd)^2}$

$\displaystyle 4 A^2 = (ab + cd)^2 - \frac{1}{4} (a^2 + b^2 -c^2 - d^2)^2$

$\displaystyle 16 A^2 = 4(ab + cd)^2 - (a^2 + b^2 -c^2 - d^2)^2$

$\displaystyle 16 A^2 = (2(ab + cd) - (a^2 + b^2 -c^2 - d^2))$

$\displaystyle (2(ab + cd) + (a^2 + b^2 -c^2 - d^2))$

$\displaystyle 16 A^2 = ((c + d)^2 - (a - b)^2)((a + b)^2 - (c - d)^2)$

$\displaystyle 16 A^2 = ((c + d) - (a - b)) ((c + d) + (a - b))$

$\displaystyle ((a + b) - (c - d)) ((a + b) + (c - d))$

$\displaystyle s = \frac{a + b + c + d}{2}$

$\displaystyle 16 A^2 = (2s - 2a) (2s - 2b) (2s - 2c) (2s - 2d)$

$\displaystyle 16 A^2 = 16 (s - a) (s - b) (s - c) (s - d)$

$\displaystyle A^2 = (s - a) (s - b) (s - c) (s - d)$

$\displaystyle \Downarrow$

$\displaystyle A = \sqrt{(s - a) (s - b) (s - c) (s - d)}$

Neste artikkel kommer i mai. Hilsen erty56.

MATTENØTT NR. 183 28. mars 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Herons formel gjelder for enhver trekant med sidene a,b og c. Den sier at arealet av trekanten er

$A = \sqrt{s (s - a)(s - b)(s - c)}$

der s er halve omkretsen av trekanten, dvs.

$s = \frac{a + b + c}{2}$

Man har en tilsvarende formel for sykliske firkanter. En syklisk firkant er en firkant med en omskrevet sirkel, dvs. at alle hjørnene i firkanten ligger på sirkelranden.

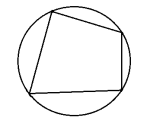
Arealet er gitt ved

$A = \sqrt{(s - a)(s - b)(s - c)(s - d)}$

der a, b, c og d er sidene i firkanten og s er halve omkretsen, dvs.

$s = \frac{a + b + c + d}{2}$

OPPGAVE 173 – FIRKANTER her på Realfagshjørnet gikk ut på å bestemme arealet til sykliske firkanter. Lenke til løsningsforslaget:

MATTENØTT NR. 174

Her kommer dagens oppgave:

OPPGAVE 183 – NOE VANSKELIG GEOMETRI

Gitt en syklisk firkant med sidene a, b, c og d. Vis at arealet er

$A = \sqrt{(s - a)(s - b)(s - c)(s - d)}$

der s er halve omkretsen.

Hint: Det finnes flere mulige løsningsforslag. Man kan f.eks. anvende vektorregning eller klassisk geometri. Utledning av en annen geometrisk formel ved vektorregning finnes her:

MATTENØTT NR. 126 + UTLEDNING NR. 125

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 182 – SVÆRT ENKEL REGNING

A) Hva blir -3 delt på -5?

$\frac{-3}{-5} = \frac{3}{5}$

B) Hva blir 2 delt på brøken 4/7?

$\frac{2}{\frac{4}{7}}$

$= \frac{2 \cdot 7}{\frac{4}{7} \cdot 7}$

$= \frac{14}{4}$

$= \frac{7}{2}$

C) Hva blir 7⁸delt på 7⁵ ?

$\frac{7^8}{7^5} = 7^{8-5} = 7^3 = 7 \cdot 7 \cdot 7 = 343$

D) Hva er 57 % av 153?

Intervallet [0 , 1] i deler tilsvarer intervallet [0 , 100] i prosent.

$153 \cdot 0,57 = 87,21$

Neste artikkel kommer i april. Hilsen erty56.

MATTENØTT NR. 182 23. februar 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 182 – SVÆRT ENKEL REGNING

A) Hva blir -3 delt på -5?

B) Hva blir 2 delt på brøken 4/7?

C) Hva blir 7⁸delt på 7⁵ ?

D) Hva er 57 % av 153?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 181 – LETT GEOMETRI IX

Gitt en rettvinklet trekant ABC, med punktet D. AD står vinkelrett på BC. Figur:

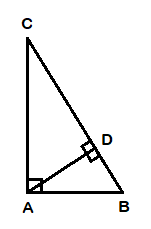
Vis at AD² = BD ⋅ DC

Løsningsforslag:

Man benytter pytagoras setning.

$AD^2 + BD^2 = AB^2 \indent \wedge \indent AD^2 + DC^2 = AC^2$

$AB^2 + AC^2 = BC^2$

$AD^2 + BD^2 + AD^2 + DC^2 = BC^2$

$2 \cdot AD^2 = BC^2 - BD^2 - DC^2$

$2 \cdot AD^2 = (BD + DC)^2 - BD^2 - DC^2$

$2 \cdot AD^2 = BD^2 + 2 \cdot BD \cdot DC + DC^2 - BD^2 - DC^2$

$2 \cdot AD^2 = 2 \cdot BD \cdot DC$

$AD^2 = BD \cdot DC$

Neste artikkel kommer i mars. Hilsen erty56.

JULENØTTER 2021 – FASIT 9. januar 2022

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer løsningsforslag til forrige måneds julenøtter:

OPPGAVE 176 – TO ENKLE TALLFØLGER

A) Gitt tallene 1, 4, 9, 16, 24, 36, 49, 64. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

Alle tallene er på formen n², der n er et naturlig tall, bortsett fra 24.

Svar: 24

B) Gitt tallene 1, 8, 26, 64, 125, 216, 343, 512. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

Alle tallene er på formen n³, der n er et naturlig tall, bortsett fra 26.

Svar: 26

OPPGAVE 177 – TO TALLFØLGER

A) Gitt tallene 2, 3/2, 4/3, 6/4, 6/5, 7/6, 8/7, 9/8. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

Alle tallene er på formen 1 + 1/n, der n er et naturlig tall fra 1 til 8 i stigende rekkefølge. Riktignok er 6/4 = 3/2, men 6/4 passer ikke inn i systemet.

Svar: 6/4

B) Gitt tallene -1, 1/2, -1/3, 1/4, -1/5, -1/6, -1/7, 1/8. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

Alle tallene er på formen $(-1)^n \frac{1}{n}$ der n er et naturlig tall, bortsett fra -1/6. (n = 6 vil gi 1/6).

Svar: -1/6

Merknad: De naturlige tallene er hele og positive tall, dvs. 1, 2, 3, …

n går fra 1 til 8 i alle disse oppgavene.

OPPGAVE 178 – LETT GEOMETRI VIII

Gitt trekanten ABC, med punktene D, E og F. Se figur:

AE = 5, EC = 3 og AD = 2. Figuren er kun en skisse. Man finner ingen opplysninger ved å måle på figuren.

A) Finn EF

Trekantene EFC og ADE er formlike, ergo er

$\displaystyle \frac{EF}{EC} = \frac{AD}{AE}$

$\displaystyle EF = \frac{AD \cdot EC}{AE} = \frac{2 \cdot 3}{5} = 1,2$

B) Finn AB

$\displaystyle AB = AD + DB = AD + EF = 2 + 1,2 = 3,2$

OPPGAVE 179 – FINN X

$\displaystyle \indent \frac{1}{x} = \frac{sin \ x}{x} \indent (x > 0)$

$\displaystyle \indent \frac{1}{x} - \frac{sin \ x}{x} = 0$

$\displaystyle \indent \frac{1 - sin \ x}{x} = 0$

$\displaystyle \indent 1 - sin \ x = 0$

$\displaystyle \indent sin \ x = 1$

$\displaystyle \Downarrow$

$\displaystyle \indent x = \frac{\pi}{2} \indent \indent$ kkkkk (1. omløp)

$\displaystyle \indent x = \frac{\pi}{2} + 2\pi n, \indent n = 0, 1, 2, ... \indent$ hhhhh (alle omløp)

OPPGAVE 180 – FØLGE MED EPSILON PÅ 1/100

Gitt følgen $\displaystyle a_n = \frac{n - 1}{n}$ . Man skal finne hvor nært følgen er 0,9 med en sikkerhet på 1/100. Svaret skal kun oppgis i naturlige tall. Hint: Man starter med:

$\displaystyle \mid \frac{n - 1}{n} - 0,9 \mid \ < \ \frac{1}{100}$

De naturlige tallene er hele og positive tall, dvs. lll $\displaystyle \indent \mathbb{N} = \{1, 2, 3, ...\}$

$\displaystyle \mid \frac{n - 1}{n} - 0,9 \mid \ < \ \frac{1}{100}$

$\displaystyle \mid 1 - \frac{1}{n} - 0,9 \mid \ < \ \frac{1}{100}$

$\displaystyle \mid - \frac{1}{n} + \frac{1}{10} \mid \ < \ \frac{1}{100}$

$\displaystyle - \frac{1}{100} \ < \ - \frac{1}{n} + \frac{1}{10} \ < \ \frac{1}{100}$

$\displaystyle - \frac{1}{n} + \frac{1}{10} + \frac{1}{100} > 0 \indent \wedge \indent - \frac{1}{n} + \frac{1}{10} - \frac{1}{100} < 0$

$\displaystyle - \frac{1}{n} + \frac{10 + 1}{100} > 0 \indent \wedge \indent - \frac{1}{n} + \frac{10 - 1}{100} < 0$

$\displaystyle - \frac{1}{n} + \frac{11}{100} > 0 \indent \wedge \indent - \frac{1}{n} + \frac{9}{100} < 0$

$\displaystyle \frac{-100 + 11n}{100n} > 0 \indent \wedge \indent \frac{-100 + 9n}{100n} < 0$

$\displaystyle -100 + 11n = 0 \indent \wedge \indent -100 + 9n = 0$

$\displaystyle 11n = 100 \indent \wedge \indent 9n = 100$

$\displaystyle n = \frac{100}{11} \indent \wedge \indent n = \frac{100}{9}$

$\displaystyle 100n = 0 \indent \Rightarrow \indent n = 0 \indent$ jjjj for begge

t64a

t64b

$\displaystyle n \in < \frac{100}{11} , \frac{100}{9} > \indent \wedge \indent n \in \mathbb{N}$

$\displaystyle \Downarrow$

$\displaystyle n \in \{10 , 11\}$

Til slutt en ny mattenøtt:

OPPGAVE 181 – LETT GEOMETRI IX

Gitt en rettvinklet trekant ABC, med punktet D. AD står vinkelrett på BC. Figur:

t64c

Vis at AD² = BD ⋅ DC

Neste artikkel kommer i februar. Godt nyttår! Hilsen erty56.

JULENØTTER 2021 12. desember 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Denne gangen kommer julenøtter i form av noen nye matematiske quiz og grublerier:

OPPGAVE 176 – TO ENKLE TALLFØLGER

A) Gitt tallene 1, 4, 9, 16, 24, 36, 49, 64. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

B) Gitt tallene 1, 8, 26, 64, 125, 216, 343, 512. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

hh

OPPGAVE 177 – TO TALLFØLGER

A) Gitt tallene 2, 3/2, 4/3, 6/4, 6/5, 7/6, 8/7, 9/8. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

B) Gitt tallene -1, 1/2, -1/3, 1/4, -1/5, -1/6, -1/7, 1/8. Et av tallene hører ikke hjemme blant de andre. Hvilket er det?

OPPGAVE 178 – LETT GEOMETRI VIII

Gitt trekanten ABC, med punktene D, E og F. Se figur:

AE = 5, EC = 3 og AD = 2. Figuren er kun en skisse. Man finner ingen opplysninger ved å måle på figuren.

A) Finn EF

B) Finn AB

OPPGAVE 179 – FINN X

$\displaystyle \indent \frac{1}{x} = \frac{sin \ x}{x} \indent (x > 0)$

OPPGAVE 180 – FØLGE MED EPSILON PÅ 1/100

Gitt følgen $\displaystyle a_n = \frac{n - 1}{n}$ . Man skal finne hvor nært følgen er 0,9 med en sikkerhet på 1/100. Svaret skal kun oppgis i naturlige tall. Hint: Man starter med:

$\displaystyle \mid \frac{n - 1}{n} - 0,9 \mid \ < \ \frac{1}{100}$

De naturlige tallene er hele og positive tall, dvs.:

$\displaystyle \mathbb{N} = \{1, 2, 3, ...\}$

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 175 – FJERDEGRADSUTTRYKK

A) Regn ut og trekk sammen

$\displaystyle (x^2 + y^2)(x + y)(x - y)$

$\displaystyle = (x^2 + y^2)(x^2 - y^2)$

$\displaystyle = (x^4 - y^4)$

B) Gitt

$\displaystyle \indent y^4 = x^4$

Finn løsningene til y.

Man benytter substitusjonen $\displaystyle y^2 = u$

$\displaystyle \indent u^2 = x^4$

$\displaystyle \indent u = \pm x^2$

$\displaystyle \indent y^2 = \pm x^2$

$\displaystyle \indent y^2 = x^2 \indent \vee \indent y^2 = -x^2$

$\displaystyle \indent y = \pm x \indent \vee \indent y = \pm \sqrt{-x^2} = \pm \sqrt{(-1) x^2} = \pm \sqrt{-1} x = \pm ix$

$\displaystyle \indent y = -x \indent \vee \indent y = x \indent \vee \indent y = -ix \indent \vee \indent y = ix$

Dette er de fire generelle løsningene til y. Det finnes uendelig mange spesialtilfeller, bl.a. y = x = 0, y = x = 1 osv. Man kan også ta utgangspunkt i A):

$\displaystyle (x^2 + y^2)(x + y)(x - y) = 0$

$\displaystyle \indent \Downarrow$

$\displaystyle (x^2 + y^2) = 0 \indent \vee \indent (x + y) = 0 \indent \vee \indent (x - y) = 0$

$\displaystyle y^2 = -x^2 \indent \vee \indent y = -x \indent \vee \indent y = x$

$\displaystyle \indent \Downarrow$

$\displaystyle \indent y = -x \indent \vee \indent y = x \indent \vee \indent y = -ix \indent \vee \indent y = ix$

Løsningsforslag til julenøttene blir lagt ut her på Realfagshjørnet i januar. God jul! Hilsen erty56.

MATTENØTT NR. 175 22. november 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 175 – FJERDEGRADSUTTRYKK

A) Regn ut og trekk sammen

$\displaystyle (x^2 + y^2)(x + y)(x - y)$

B) Gitt

$\displaystyle \indent y^4 = x^4$

Finn løsningene til y.

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 174 – LIGNINGER OG POTENSER

A) Gitt

Finn x og y.

$\displaystyle x^2 - 3x + 2 = 0$

$\displaystyle (x - \frac{3}{2})^2 = -2 + (-\frac{3}{2})^2$

$\displaystyle (x - \frac{3}{2})^2 = \frac{1}{4}$

$\displaystyle \sqrt{(x - \frac{3}{2})^2} = \sqrt{\frac{1}{4}}$

$\displaystyle x - \frac{3}{2} = \pm \frac{1}{2}$

$\displaystyle x = \pm \frac{1}{2} + \frac{3}{2}$

$\displaystyle x = 1 \indent \vee \indent x = 2$

$\displaystyle x + y = 3$

$\displaystyle y = 3 - x$

$\displaystyle x = 1 \indent \wedge \indent y = 3 - x = 3 - 1 = 2$

$\displaystyle x = 2 \indent \wedge \indent y = 3 - x = 3 - 2 = 1$

B) Regn ut

Begge løsningene (x , y) = (1, 2) og (x , y) = (2 , 1) gir det samme svaret

$\displaystyle x^2 + y^2 = 1^2 + 2^2 = 1 + 4 = 5$

C) Regn ut

Begge løsningene (x , y) = (1, 2) og (x , y) = (2 , 1) gir det samme svaret

$\displaystyle x^5 + y^5 = 1^5 + 2^5 = 1 + 32 = 33$

Julenøtter kommer i desember. Hilsen erty56.

MATTENØTT NR. 173 25. september 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 173 – FIRKANTER

A) Gitt en syklisk firkant med sider 9, 10, 10 og 21. Hva blir arealet av firkanten?

B) Gitt en syklisk firkant med sider 15, 24, 7 og 20. Hva blir arealet av firkanten?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 172 – FJERDEGRADSLIGNINGER

A) Løs ligningen

$\displaystyle x^4 - 5x^2 + 4 = 0$

Man benytter substitusjonen $\displaystyle x^2 = y$

$\displaystyle y^2 - 5y + 4 = 0$

$\displaystyle (y - \frac{5}{2})^2 = -4 + (-\frac{5}{2})^2$

$\displaystyle (y - \frac{5}{2})^2 = \frac{9}{4}$

$\displaystyle \sqrt{(y - \frac{5}{2})^2} = \sqrt{\frac{9}{4}}$

$\displaystyle y - \frac{5}{2} = \pm \frac{3}{2}$

$\displaystyle y = \frac{5}{2} \pm \frac{3}{2}$

$\displaystyle y = 4 \indent \vee \indent y = 1$

$\displaystyle \Downarrow$

$\displaystyle x^2 = 4 \indent \vee \indent x^2 = 1$

$\displaystyle x = \pm 2 \indent \vee \indent x = \pm 1$

$\displaystyle x = -1 \indent \vee \indent x = 1 \indent \vee \indent x = -2 \indent \vee \indent x = 2$

B) Løs ligningen

$\displaystyle x^4 + 5x^2 + 4 = 0$

Man benytter substitusjonen $\displaystyle x^2 = y$

$\displaystyle y^2 + 5y + 4 = 0$

$\displaystyle (y + \frac{5}{2})^2 = -4 + (\frac{5}{2})^2$

$\displaystyle (y + \frac{5}{2})^2 = \frac{9}{4}$

$\displaystyle \sqrt{(y + \frac{5}{2})^2} = \sqrt{\frac{9}{4}}$

$\displaystyle y + \frac{5}{2} = \pm \frac{3}{2}$

$\displaystyle y = -\frac{5}{2} \pm \frac{3}{2}$

$\displaystyle y = -4 \indent \vee \indent y = -1$

$\displaystyle \Downarrow$

$\displaystyle x^2 = -4 \indent \vee \indent x^2 = -1$

$\displaystyle x = \pm 2i \indent \vee \indent x = \pm i$

$\displaystyle x = -i \indent \vee \indent x = i \indent \vee \indent x = -2i \indent \vee \indent x = 2i$

Merknad: $\displaystyle i = \sqrt{-1}$

Neste artikkel kommer i oktober. Hilsen erty56.

MATTENØTT NR. 172 21. august 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 172 – FJERDEGRADSLIGNINGER

A) Løs ligningen

$\displaystyle x^4 - 5x^2 + 4 = 0$

B) Løs ligningen

$\displaystyle x^4 + 5x^2 + 4 = 0$

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 171 – GJENNOMSNITT

Gitt 50 tall med gjennomsnittet 102. 10 av tallene har gjennomsnittet 10. Hva blir gjennomsnittet til de resterende 40 tallene?

Oppgaveteksten gir:

$\displaystyle \frac{10 \cdot 10 + 40 \cdot x}{50} = 102$

$\displaystyle 100 + 40x = 5100$

$\displaystyle 40x = 5000$

$\displaystyle x = 125$

Svar: De resterende 40 tallene har gjennomsnittet 125.

Neste artikkel kommer i september. Hilsen erty56.

MATTENØTT NR. 171 22. juli 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 171 – GJENNOMSNITT

Gitt 50 tall med gjennomsnittet 102. 10 av tallene har gjennomsnittet 10. Hva blir gjennomsnittet til de resterende 40 tallene?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 170 – STØRSTE OG MINSTE TALL

A) Gitt tallene

$\displaystyle 4^{-2} \ , \ 2^{-3} \ , \ 8^{-1} \ , \ 2^{-4} \ , \ 8^{-2} \ , \ 4^{-1}$

Hvilket av tallene er minst?

$\displaystyle 4^{-2} = \frac{1}{4^2} = \frac{1}{16} \ , \ 2^{-3} = \frac{1}{2^3} = \frac{1}{8}$

$\displaystyle 8^{-1} = \frac{1}{8} \ , \ 2^{-4} = \frac{1}{2^4} = \frac{1}{16}$

$\displaystyle 8^{-2} = \frac{1}{8^2} = \frac{1}{64} \ , \ 4^{-1} = \frac{1}{4}$

$\displaystyle \frac{1}{64} < \frac{1}{16} < \frac{1}{8} < \frac{1}{4}$

Svar:

$\displaystyle 8^{-2}$

B) Gitt tallene

$\displaystyle \sqrt[5]{5!}$

$\displaystyle \sqrt[6]{6!}$

Hvilket av tallene er størst?

Antar

$\displaystyle \sqrt[6]{6!} > \sqrt[5]{5!}$

$\displaystyle (6!)^{1/6} > (5!)^{1/5}$

$\displaystyle ln ((6!)^{1/6}) > ln ((5!)^{1/5})$

$\displaystyle \frac{1}{6} ln (6!) > \frac{1}{5} ln (5!)$

$\displaystyle \frac{1}{6} ln (6 \cdot 5!) > \frac{1}{5} ln (5!)$

$\displaystyle \frac{1}{6} (ln \ 6 + ln \ 5!) > \frac{1}{5} ln (5!)$

$\displaystyle \frac{1}{6} (ln \ 6) > \frac{1}{30} ln (5!)$

$\displaystyle 5 \cdot (ln \ 6) > ln (5!)$

$\displaystyle ln \ 6^5 > ln (5!)$

$\displaystyle e^{ln \ 6^5} > e^{ln (5!)}$

$\displaystyle 6^5 > 5!$

$\displaystyle 6 \cdot 6 \cdot 6 \cdot 6 \cdot 6 > 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$

Antagelsen var riktig. Altså er

$\displaystyle \sqrt[6]{6!}$

størst.

Neste artikkel kommer i august. Hilsen erty56.

MATTENØTT NR. 170 22. juni 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 170 – STØRSTE OG MINSTE TALL

A) Gitt tallene

$\displaystyle 4^{-2} \ , \ 2^{-3} \ , \ 8^{-1} \ , \ 2^{-4} \ , \ 8^{-2} \ , \ 4^{-1}$

Hvilket av tallene er minst?

B) Gitt tallene

$\displaystyle \sqrt[5]{5!}$

$\displaystyle \sqrt[6]{6!}$

Hvilket av tallene er størst?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 169 – ENKEL REKKE

En tallfølge er geometrisk dersom hvert ledd (bortsett fra det første) er lik leddet foran multiplisert med et fast tall. Dette tallet er tallfølgens kvotient k. En slik følge kan skrives

$\displaystyle a_1 \ , \ a_1 k \ , \ a_1 k^2 \ , ... , \ a_1 k^{n - 2} \ , \ a_1 k^{n - 1}$

A) Gitt den geometriske følgen

$\displaystyle 1 \ , \ 2 \ , \ 4 \ , ... , \ 256 \ , \ 512$

med 10 ledd. Hva blir kvotienten k ?

$\displaystyle a_1 = 1 \indent \wedge \indent a_1 k = 2$

$\displaystyle \Downarrow$

$\displaystyle k = 2$

B) Hva blir ledd nr. 5 og nr. 7 ?

Man kan skrive følgen:

$\displaystyle 1 \ , \ 2 \ , \ 4 \ , \ 8 \ , \ 16 \ , \ 32 \ , \ 64 \ , \ 128 \ , \ 256 \ , \ 512$

Ledd nr. 5 blir 16 og ledd nr. 7 blir 64

Dersom man legger sammen alle ledd i en følge får man en rekke. En generell geometrisk rekke kan skrives

$\displaystyle a_1 \ + \ a_1 k \ + \ a_1 k^2 \ + \ ... \ + \ a_1 k^{n - 2} \ + \ a_1 k^{n - 1}$

C) Gitt den geometriske rekken

$\displaystyle 1 \ + \ 2 \ + \ 4 \ + \ ... \ + \ 256 \ + \ 512$

med 10 ledd. Hva blir rekkens sum?

$\displaystyle \sum = 1 \cdot \frac{2^{10} - 1}{2 - 1} = \frac{1024 - 1}{1} = 1023$

Neste artikkel kommer i juli. Hilsen erty56.

MATTENØTT NR. 169 20. mai 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 169 – ENKEL REKKE

En tallfølge er geometrisk dersom hvert ledd (bortsett fra det første) er lik leddet foran multiplisert med et fast tall. Dette tallet er tallfølgens kvotient k. En slik følge kan skrives

$\displaystyle a_1 \ , \ a_1 k \ , \ a_1 k^2 \ , ... , \ a_1 k^{n - 2} \ , \ a_1 k^{n - 1}$

A) Gitt den geometriske følgen

$\displaystyle 1 \ , \ 2 \ , \ 4 \ , ... , \ 256 \ , \ 512$

med 10 ledd. Hva blir kvotienten k ?

B) Hva blir ledd nr. 5 og nr. 7 ?

Dersom man legger sammen alle ledd i en følge får man en rekke. En generell geometrisk rekke kan skrives

$\displaystyle a_1 \ + \ a_1 k \ + \ a_1 k^2 \ + \ ... \ + \ a_1 k^{n - 2} \ + \ a_1 k^{n - 1}$

C) Gitt den geometriske rekken

$\displaystyle 1 \ + \ 2 \ + \ 4 \ + \ ... \ + \ 256 \ + \ 512$

med 10 ledd. Hva blir rekkens sum?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 168 – VANSKELIG OPPGAVE II

A) Regn ut summen

Man setter først

$\displaystyle \sum\limits_{x=1}^{n} 4 \cdot x^3$

$\displaystyle = 4 \cdot \sum\limits_{x=1}^{n} x^3$

Man kan finne summen ved å regne en differensligning, hvor man betrakter differensen mellom ledd nr. n og nr. n+1

$\displaystyle x_{n+1} - x_n = (n + 1)^3 = n^3 + 3n^2 + 3n + 1$

$\displaystyle x_{n + 1} - x_n = 0$

$\displaystyle r - 1 = 0$

$\displaystyle r = 1$

$\displaystyle x_n^h = F \cdot 1^n = F$

$\displaystyle x_n^p = An^4 + Bn^3 + Cn^2 + Dn + E$

$\displaystyle A(n + 1)^4 + B(n + 1)^3 + C(n + 1)^2 + D(n + 1) + E$

$\displaystyle - (An^4 + Bn^3 + Cn^2 + Dn + E)$

$\displaystyle = n^3 + 3n^2 + 3n + 1$

$\displaystyle A(n^4 + 4n^3 + 6n^2 + 4n + 1) + B(n^3 + 3n^2 + 3n + 1)$

$\displaystyle + C(n^2 + 2n + 1) + D(n + 1) + E$

$\displaystyle - (An^4 + Bn^3 + Cn^2 + Dn + E)$

$\displaystyle = n^3 + 3n^2 + 3n + 1$

$\displaystyle A - A = 0$

$\displaystyle 0A = 0$

$\displaystyle 4A + B - B = 1$

$\displaystyle 4A = 1$

$\displaystyle 6A + 3B + C - C = 3$

$\displaystyle 6A + 3B = 3$

$\displaystyle 4A + 3B + 2C + D - D = 3$

$\displaystyle 4A + 3B + 2C = 3$

$\displaystyle A + B + C + D + E - E = 1$

$\displaystyle A + B + C + D = 1$

$\displaystyle 4A = 1$

$\displaystyle A = \frac{1}{4}$

$\displaystyle 6A + 3B = 3$

$\displaystyle 3B = 3 - 6A = 3 - 6 \cdot \frac{1}{4} = \frac{3}{2}$

$\displaystyle B = \frac{1}{2}$

$\displaystyle 4A + 3B + 2C = 3$

$\displaystyle 2C = 3 - 4A - 3B$

$\displaystyle = 3 - 4 \cdot \frac{1}{4} - 3 \cdot \frac{1}{2} = \frac{1}{2}$

$\displaystyle C = \frac{1}{4}$

$\displaystyle A + B + C + D = 1$

$\displaystyle D = 1 - A - B - C = 1 - \frac{1}{4} - \frac{1}{2} - \frac{1}{4} = 0$

$\displaystyle x_n^p = An^4 + Bn^3 + Cn^2 + Dn + E$

$\displaystyle = \frac{1}{4} n^4 + \frac{1}{2} n^3 + \frac{1}{4} n^2 + E$

$\displaystyle x_n = x_n^h + x_n^p$

$\displaystyle = F + \frac{1}{4} n^4 + \frac{1}{2} n^3 + \frac{1}{4} n^2 + E$

$\displaystyle x_1 = 1$

$\displaystyle F + \frac{1}{4} \cdot 1^4 + \frac{1}{2} \cdot 1^3 + \frac{1}{4} \cdot 1^2 + E = 1$

$\displaystyle F + \frac{1}{4} + \frac{1}{2} + \frac{1}{4} + E = 1$

$\displaystyle F + E = 0$

$\displaystyle \Downarrow$

$\displaystyle x_n = \frac{1}{4} n^4 + \frac{1}{2} n^3 + \frac{1}{4} n^2$

$\displaystyle = \frac{1}{4} n^2 (n^2 + 2n + 1) = \frac{1}{4} n^2 (n + 1)^2$

Altså er

$\displaystyle \sum\limits_{x=1}^{n} x^3$

$\displaystyle = \frac{1}{4} n^2 (n + 1)^2$

Dette gir summen

$\displaystyle \sum\limits_{x=1}^{n} 4 \cdot x^3$

$\displaystyle = 4 \cdot \sum\limits_{x=1}^{n} x^3$

$\displaystyle = 4 \cdot \frac{1}{4} n^2 (n + 1)^2$

$\displaystyle = n^2 (n + 1)^2$

B) Beregn grenseverdien

\displaystyle \lim\limits_{n \to \infty} \frac{4 \cdot 1^3 + 4 \cdot 2^3 + ... + 4 \cdot n^3}{5 n^4}

$\displaystyle = \lim\limits_{n \to \infty} \frac{n^2 (n + 1)^2}{5n^4}$

$\displaystyle = \lim\limits_{n \to \infty} \frac{n^4 + 2n^3 + n^2}{5n^4}$

$\displaystyle = \lim\limits_{n \to \infty} \frac{\frac{n^4}{n^4} + \frac{2n^3}{n^4} + \frac{n^2}{n^4}}{\frac{5n^4}{n^4}}$

$\displaystyle = \lim\limits_{n \to \infty} \frac{1 + \frac{2}{n} + \frac{1}{n^2}}{5}$

$\displaystyle = \frac{1 + 0 + 0}{5} = \frac{1}{5}$

Neste artikkel kommer i juni. Hilsen erty56.

MATTENØTT NR. 168 15. april 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 168 – VANSKELIG OPPGAVE II

A) Regn ut summen

B) Beregn grenseverdien

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 167 – REKKER MED PARTALL OG ODDETALL

Gitt to rekker som begge har n antall ledd. Den ene med partall og den andre med oddetall. Disse kan skrives på følgende måte.

Rekken med de n første partall

$\displaystyle \sum\limits_{k=1}^{n} 2k = 2 + 4 + 6 + ... + 2n$

Rekken med de n første oddetall

$\displaystyle \sum\limits_{k=1}^{n} 2k - 1 = 1 + 3 + 5 + ... + 2n - 1$

Man kan finne summen av disse rekkene ved å beregne gjennomsnittet av leddene og multiplisere dette med antall ledd.

A) Hva blir summen til rekken av partallene?

$\displaystyle \sum\limits_{k=1}^{n} 2k = 2 + 4 + 6 + ... + 2n$

$\displaystyle \sum\limits_{k=1}^{n} 2k = \frac{2 + 2n}{2} \cdot n = \frac{2 (1 + n)}{2} \cdot n = n (n + 1)$

B) Hva blir summen til rekken av oddetallene?

$\displaystyle \sum\limits_{k=1}^{n} 2k - 1 = 1 + 3 + 5 + ... + 2n - 1$

$\displaystyle \sum\limits_{k=1}^{n} 2k - 1 = \frac{1 + 2n - 1}{2} \cdot n = \frac{2n}{2} \cdot n = n^2$

C) Anta at n er det samme tallet i A) og B). Hvilken av de to rekkene har størst sum?

Siden n er det samme tallet i både A) og B) er alltid

$\displaystyle n (n + 1) > n^2$

$\displaystyle n^2 + n > n^2$

Konklusjon: Rekken av partall har størst sum.

n kan imidlertid være hvilket som helst naturlig tall $\mathbb{N}$ . De naturlige tallene er hele og positive tall. Mengden kan skrives

$\displaystyle \mathbb{N} = \{1 , 2 , 3 , ... \}$

Hint: Se OPPGAVE 71 – FINN SUMMEN i artikkelen:

FØLGER, REKKER OG GJENNOMSNITT

Her står også svaret på B)

Neste artikkel kommer i mai. Hilsen erty56.

MATTENØTT NR. 167 22. mars 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 167 – REKKER MED PARTALL OG ODDETALL

Gitt to rekker som begge har n antall ledd. Den ene med partall og den andre med oddetall. Disse kan skrives på følgende måte.

Rekken med de n første partall

$\displaystyle \sum\limits_{k=1}^{n} 2k = 2 + 4 + 6 + ... + 2n$

Rekken med de n første oddetall

$\displaystyle \sum\limits_{k=1}^{n} 2k - 1 = 1 + 3 + 5 + ... + 2n - 1$

Man kan finne summen av disse rekkene ved å beregne gjennomsnittet av leddene og multiplisere dette med antall ledd.

A) Hva blir summen til rekken av partallene?

B) Hva blir summen til rekken av oddetallene?

C) Anta at n er det samme tallet i A) og B). Hvilken av de to rekkene har størst sum?

Hint: Se OPPGAVE 71 – FINN SUMMEN i artikkelen:

FØLGER, REKKER OG GJENNOMSNITT

Her står også svaret på B)

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 166 – ENKEL NØTT

Per er halvparten så gammel som faren sin. For noen år siden var de henholdsvis 8 og 31 år. Hva er alderen deres idag?

Kaller Per sin alder for x og faren sin alder for 2x (x:2x = 1:2, altså halvparten). Setter at det har gått y år siden de var henholdsvis 8 og 31 år. Dette gir:

31 + y = 2x

8 + y = x

y = x – 8

31 + x – 8 = 2x

x = 23

2x = 46

Svar: Per er 23 år og faren 46 år idag.

Neste artikkel kommer i april. Hilsen erty56.

MATTENØTT NR. 166 23. februar 2021

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 166 – ENKEL NØTT

Per er halvparten så gammel som faren sin. For noen år siden var de henholdsvis 8 og 31 år. Hva er alderen deres idag?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 165 – VANSKELIG OPPGAVE

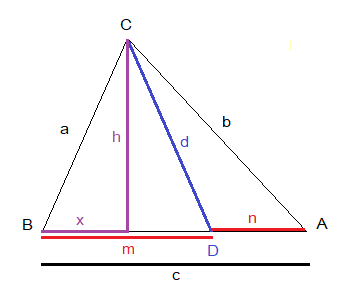
Gitt følgende trekant ABC

a, b og c er motstående sider til hjørnene A, B, og C. Det er tegnet en blå linje d til siden c. Denne deler siden c i to deler m og n(tegnet i rødt). Stewarts teorem sier at

$\displaystyle a^2 n + b^2 m = c(d^2 + mn)$

Bevis dette teoremet.

Først en ny figur:

$\displaystyle x^2 + h^2 = a^2$

$\displaystyle (m - x)^2 + h^2 = d^2$

$\displaystyle (m - x + n)^2 + h^2 = b^2$

$\displaystyle m + n = c$

$\displaystyle (c - x)^2 + h^2 = b^2$

$\displaystyle h^2 = a^2 - x^2$

$\displaystyle (m - x)^2 + a^2 - x^2 = d^2$

$\displaystyle m^2 - 2mx + x^2 + a^2 - x^2 = d^2$

$\displaystyle m^2 - 2mx + a^2 = d^2$

$\displaystyle x = \frac{d^2 - a^2 - m^2}{-2m}$

$\displaystyle (c - x)^2 + a^2 - x^2 = b^2$

$\displaystyle c^2 - 2cx + x^2 + a^2 - x^2 = b^2$

$\displaystyle c^2 - 2cx + a^2 = b^2$

$\displaystyle x = \frac{b^2 - a^2 - c^2}{-2c}$

$\displaystyle x = x$

$\displaystyle \frac{d^2 - a^2 - m^2}{-2m} = \frac{b^2 - a^2 - c^2}{-2c}$

$\displaystyle -2c (d^2 - a^2 - m^2) = -2m (b^2 - a^2 - c^2)$

$\displaystyle 2c (-d^2 + a^2 + m^2) = 2m (-b^2 + a^2 + c^2)$

$\displaystyle -2cd^2 + 2ca^2 + 2cm^2 = -2mb^2 + 2ma^2 + 2mc^2$

$\displaystyle -2cd^2 + 2a^2(c - m) + 2mb^2 = 2mc^2 - 2cm^2$

$\displaystyle -2cd^2 + 2a^2n + 2mb^2 = 2mc (c - m)$

$\displaystyle 2a^2n + 2mb^2 = 2cd^2 + 2mnc$

$\displaystyle a^2n + mb^2 = c(d^2 + mn)$

$\displaystyle a^2 n + b^2 m = c(d^2 + mn)$

Neste artikkel kommer i mars. Hilsen erty56.

JULENØTTER 2020 14. desember 2020

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Denne gangen kommer julenøtter i form av noen nye matematiske quiz og grublerier:

OPPGAVE 160 – MYNT OG KRONE

Man kaster et kronestykke 2 ganger. Det lander på krone eller mynt.

A) Hva er sannsynligheten for å få krone begge 2 ganger?

B) Hva er sannsynligheten for å få mynt og krone en gang hver?

OPPGAVE 161 – ENKELT REGNESTYKKE

Regn ut produktet

$\displaystyle (\sqrt{3} + \sqrt{3} - \sqrt{3})(\sqrt{4} - \sqrt{4} + \sqrt{4})(\sqrt{3} - \sqrt{3} + \sqrt{3})$

OPPGAVE 162 – BANKINNSKUDD

Et beløp på 10.000 kr settes inn på en bankkonto. Renten er 5 % de første 5 årene. Deretter 7 % de neste 3 årene, og deretter 4 % i 2 år. Hva har beløpet vokst til i løpet av disse 10 årene?

OPPGAVE 163 – PARABEL

Gitt annengradsfunksjonen

$\displaystyle f(x) = x^2 + bx + c$

med bunnpunkt i (1 , 0). Finn b og c.

Hint: Se

ANNENGRADSLIGNINGER OG PARABELEN

OPPGAVE 164 – LIGNINGER OG LINJER

Gitt to ligninger med to ukjente på generell form

$\displaystyle ax + by + c = 0$

$\displaystyle dx + ey + f = 0$

To slike ligninger kan tegnes som to linjer i planet på tre forskjellige måter. Linjene er tegnet i blått på alle illustrasjonene.

1) Et krysningspunkt (x , y)

2) Parallelle og ikke-sammenfallende linjer

3) Parallelle og sammenfallende linjer

Ligningene har tre mulige løsninger:

A) Ingen løsning

B) Uendelig mange løsninger

C) En løsning

Hvilke av illustrasjonene 1), 2) og 3) tilsvarer A) B) og C) ?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 159 – TALLFØLGE

Gitt en følge av tall der det første tallet er 2. Følgen er gitt ved

$\displaystyle x_{n + 1} = x_n + 1 \indent der \ x_1= 2 \indent (n \ge 1)$

a) Finn tallene

$\displaystyle x_2 \ , \ x_3 \ , \ x_4 \ og \ x_5$

Dette er en rekursjonsformel der man alltid kan finne tallet $x_{n+1}$ , dersom man kjenner verdien av leddet foran $x_n$

Svaret blir

$\displaystyle x_2 = x_1 + 1 = 2 + 1 = 3$

$\displaystyle x_3 = x_2 + 1 = 3 + 1 = 4$

$\displaystyle x_4 = x_3 + 1 = 4 + 1 = 5$

$\displaystyle x_5 = x_4 + 1 = 5 + 1 = 6$

b) Finn produktet

$\displaystyle x_1 x_2 x_3 x_4 x_5 = 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 = 720$

Merknad: Man kan også regne en såkalt differensligning, og vil få svaret

$\displaystyle x_n = 1 + n$

Da kan man direkte finne $x_n$ for enhver n.

Løsningsforslag til julenøttene blir lagt ut her på Realfagshjørnet i januar. God jul! Hilsen erty56.

MATTENØTT NR. 158 22. oktober 2020

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 158 – INTEGRASJON

Regn ut integralet

$\displaystyle \int _{3}^{8} \frac{1}{1 + \sqrt{x + 1}} \ dx$

Hint: Benytt substitusjonen

$\displaystyle u = \sqrt{x + 1}$

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 157 – LETT GEOMETRI VII

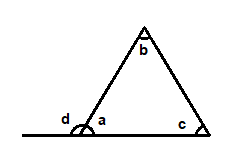
Gitt en trekant som på figuren under.

Den har tre vinkler a, b og c. Den ytre vinkelen til a er d. Summen av vinklene b og c er 120°. Hvor mange grader er vinklene a og d?

Summen av vinklene i en trekant er alltid 180°

a + b + c = 180°

a = 180° – (b + c)

a = 180° – (120°)

a = 60°

Summen av en indre og ytre vinkel langs en linje er alltid 180°

a + d = 180°

d = 180° – a

d = 180° – 60°

d = 120°

Neste artikkel kommer i november. Hilsen erty56.

MATTENØTT NR. 157 23. september 2020

Posted by erty56 in Matematikk, Populærvitenskap generelt, quiz og grublerier.
Tags: matematikk nøtter, matte nøtter, matte quiz, mattenøtter
add a comment

Hei igjen!

Her kommer en ny mattenøtt:

OPPGAVE 157 – LETT GEOMETRI VII

Gitt en trekant som på figuren under.

Den har tre vinkler a, b og c. Den ytre vinkelen til a er d. Summen av vinklene b og c er 120°. Hvor mange grader er vinklene a og d?

Her kommer løsningsforslag til forrige måneds:

OPPGAVE 156 – ANNENGRADSLIGNING

Gitt annengradsligningen

$\displaystyle ax^2 + bx + c = 0$

Den har to løsninger. Summen av løsningene er 3. Produktet av løsningene er 2.

1) Finn a, b og c.

Man skriver først opp ligningen på såkalt redusert form ved å dividere med a:

$\displaystyle ax^2 + bx + c = 0$

$\displaystyle \frac{a}{a} x^2 + \frac{b}{a} x + \frac{c}{a} = \frac{0}{a}$

$\displaystyle x^2 + \frac{b}{a} x + \frac{c}{a} = 0$

Følgende sammenheng mellom løsningene og koeffisientene gjelder alltid:

$\displaystyle x_1 + x_2 = - \frac{b}{a} \indent \wedge \indent x_1 x_2 = \frac{c}{a}$

Ifølge oppgaveteksten er:

$\displaystyle x_1 + x_2 = 3 \indent \wedge \indent x_1 x_2 = 2 \indent (*)$

Dette gir

$\displaystyle - \frac{b}{a} = 3 \indent \wedge \indent \frac{c}{a} = 2$

$\displaystyle \frac{b}{a} = -3 \indent \wedge \indent \frac{c}{a} = 2$

$\displaystyle \Downarrow$

$\displaystyle x^2 + \frac{b}{a} x + \frac{c}{a} = x^2 + (-3) x + 2 = x^2 - 3x + 2$

Svar: a = 1, b = – 3 og c = 2

2) Finn selve løsningene.

Man kan enten bruke (*), eller bare regne:

$\displaystyle x^2 - 3x + 2 = 0$

$\displaystyle (x - \frac{3}{2})^2 = -2 + (-\frac{3}{2})^2$

$\displaystyle (x - \frac{3}{2})^2 = -2 + \frac{9}{4}$

$\displaystyle (x - \frac{3}{2})^2 = \frac{9 + 4(-2)}{4}$

$\displaystyle (x - \frac{3}{2})^2 = \frac{9 - 8}{4}$

$\displaystyle (x - \frac{3}{2})^2 = \frac{1}{4}$

$\displaystyle \sqrt{(x - \frac{3}{2})^2} = \sqrt{\frac{1}{4}}$

$\displaystyle x - \frac{3}{2} = \pm \frac{1}{2}$

$\displaystyle x = \frac{3}{2} \pm \frac{1}{2}$

$\displaystyle \Downarrow$

$\displaystyle x_1 = \frac{3}{2} + \frac{1}{2} = 2 \indent \vee \indent x_2 = \frac{3}{2} - \frac{1}{2} = 1$

Her er mer info om annengradsligninger:

ANNENGRADSLIGNINGER OG PARABELEN

Neste artikkel kommer i oktober. Hilsen erty56.

« older posts newer posts »

Realfagshjørnet

MATTENØTT NR. 187 27. juli 2022

MATTENØTT NR. 186 26. juni 2022

MATTENØTT NR. 185 21. mai 2022

MATTENØTT NR. 184 20. april 2022

MATTENØTT NR. 183 28. mars 2022

MATTENØTT NR. 182 23. februar 2022

JULENØTTER 2021 – FASIT 9. januar 2022

JULENØTTER 2021 12. desember 2021

MATTENØTT NR. 175 22. november 2021

MATTENØTT NR. 173 25. september 2021

MATTENØTT NR. 172 21. august 2021

MATTENØTT NR. 171 22. juli 2021

MATTENØTT NR. 170 22. juni 2021

MATTENØTT NR. 169 20. mai 2021

MATTENØTT NR. 168 15. april 2021

MATTENØTT NR. 167 22. mars 2021

MATTENØTT NR. 166 23. februar 2021

JULENØTTER 2020 14. desember 2020

MATTENØTT NR. 158 22. oktober 2020

MATTENØTT NR. 157 23. september 2020

Kategorier

Arkiv

Feeds

Realfagshjørnet

MATTENØTT NR. 187 27. juli 2022

Del dette:

MATTENØTT NR. 186 26. juni 2022

Del dette:

MATTENØTT NR. 185 21. mai 2022

Del dette:

MATTENØTT NR. 184 20. april 2022

Del dette:

MATTENØTT NR. 183 28. mars 2022

Del dette:

MATTENØTT NR. 182 23. februar 2022

Del dette:

JULENØTTER 2021 – FASIT 9. januar 2022

Del dette:

JULENØTTER 2021 12. desember 2021

Del dette:

MATTENØTT NR. 175 22. november 2021

Del dette:

MATTENØTT NR. 173 25. september 2021

Del dette:

MATTENØTT NR. 172 21. august 2021

Del dette:

MATTENØTT NR. 171 22. juli 2021

Del dette:

MATTENØTT NR. 170 22. juni 2021

Del dette:

MATTENØTT NR. 169 20. mai 2021

Del dette:

MATTENØTT NR. 168 15. april 2021

Del dette:

MATTENØTT NR. 167 22. mars 2021

Del dette:

MATTENØTT NR. 166 23. februar 2021

Del dette:

JULENØTTER 2020 14. desember 2020

Del dette:

MATTENØTT NR. 158 22. oktober 2020

Del dette:

MATTENØTT NR. 157 23. september 2020

Del dette:

Kategorier

Arkiv

Blogroll

Feeds